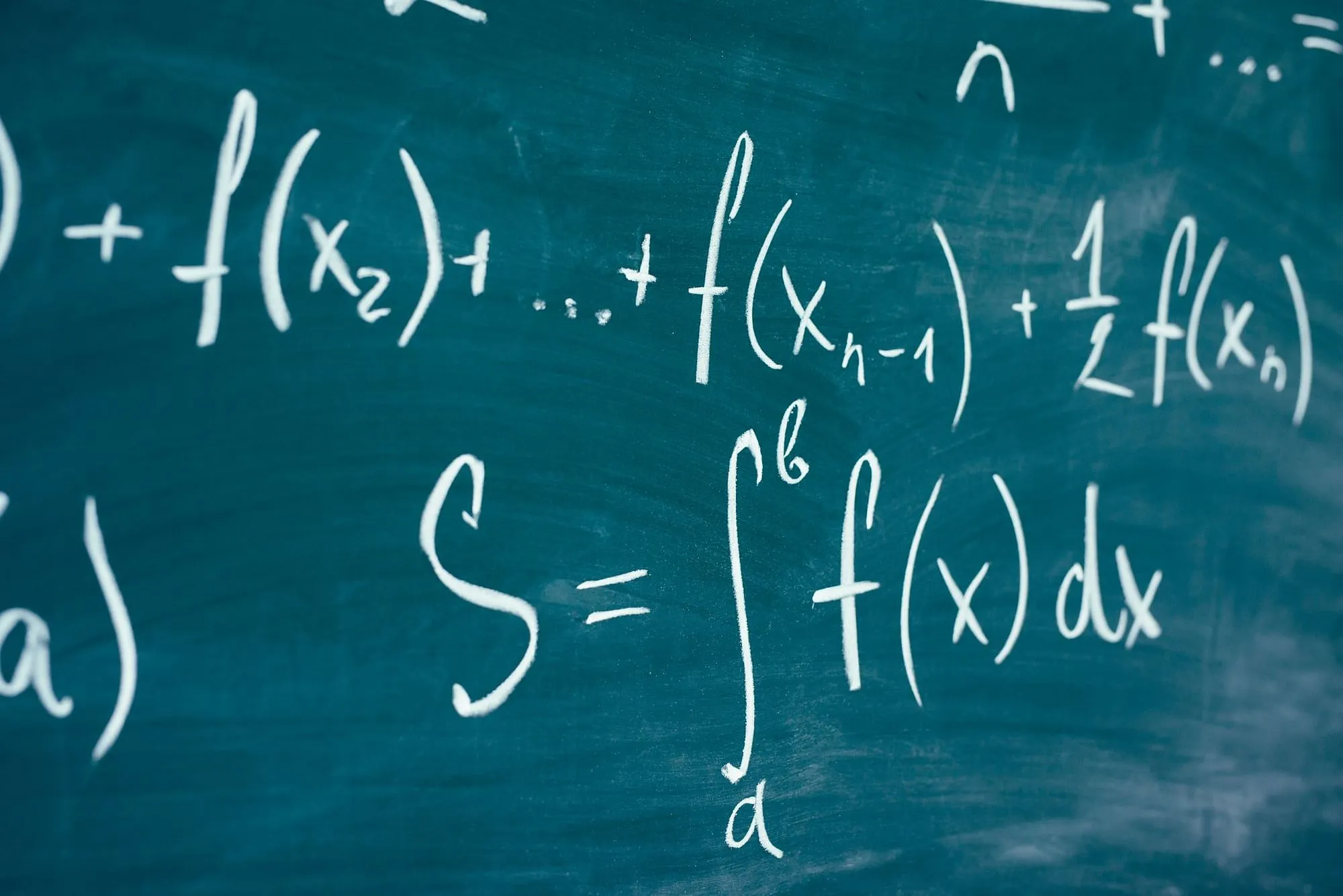It was a sunny day of mid-summer. I left for University to attend my day-long academic stuff. As the class concluded, I looked for a friend. I came to know from my class mates that he had not attend the class, because of today’s supplementary examination. As I stepped out from the academic block, my phone rang up. It was the same friend. He told me to meet immediately in the backyard of academic block.
After a few minutes, I along with two other friends, found him in a state of distress. What is the matter? In reply, he expressed his concern that he has not cleared all concepts of Calculus. I told him to sit down, and tried my best to make him understand some basics of Calculus, so that he can get deal with the questions based on Calculus. My two other friends chipped in. Finally the session of our practice concluded and he left for attending the examination. Hours later, as he was stepping out from the examination hall, he was looking very happy.
What actually fails majority of students in mathematics, is a phobia especially when it comes to Calculus in higher order engineering mathematics. Calculus is a simple mathematical operation like we have studied Addition, Subtraction, Multiplication, and Division, and these signs have their own mathematical operations. The operation is crystal clear, as in addition we add the numbers, in subtraction we subtract the numbers, in multiplication we multiply the numbers and in division we divide the numbers. And all these operations have certain rules to follow for their result outcome.
As students looks towards the unit of Calculus, they are afraid of Delta and integral based signs along with a mathematical function. Calculus is nothing but two mathematical operations namely “Differentiation” and “Integration” in a fraction of for differentiation and for Integration. While dealing with such kind of questions, the student should not say why? & what? But should say how? How do these two operations work? What they represent? What are the rules for their operation? How can we apply these rules?
Illustration
Let’s consider, if we have a bucket of water with a tap fitted in the bottom. If we turn the tap, we will observe the water spurt out faster, and after a few minutes, the level of water in the bucket is dipping and there would be a gradual change in its speed. Hence the amount of water spurting out in each second is a rate of change, that is the differentiation of the amount of water in the bucket with respect to time. So when the bucket was full, we have high rate of change and when its level was dipping, we observe we have a low rate of change and we write it mathematically as.
Now in the second case, if we collect this water which is spurting out through the tap in another empty bucket, obviously the amount of water in the bucket will increase with time. However, this is not easy to know and estimate how much water is falling into the bucket with time. If we consider that in the first second it was a quart of water. But now we can’t say that there will be two quarts of water for 2nd second. So we have to adjust our calculation with the rate of flow in the 2nd second. However, still our calculation is not accurate, as there are different flows in different quarters. Hence the term “Integration” is the process where we have to sum up all intervals between the summation, so we come closer to the true and accurate results. If is the rate of flow and (V) is volume of water in (T) Seconds, so (V) is the integral which will evaluated over [0, t]
In a nut-shell we can say Differentiation and integration are two different poles.